Art Definitions, Glossary of Terms |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Page 09 / 09
Freehand Drawing Book DEFINITIONS.Aesthetics. The science which treats of the beautiful, and its various modes of representation in Nature and art ; the philosophy of the fine arts. Accent. Emphasis of light or of dark in a light-and-shade drawing ; of dark in an outline drawing ; and of color or of light and dark in a color sketch. Altitude. The perpendicular distance between the bases, or between the vertex and the base, of a solid or plane figure. Angle. The difference in direction of two lines which meet or tend to meet. The lines are called the sides, and the point of meeting, the vertex of the angle.
Apex. The summit or highest point of an object. Appearance. The image produced in the eye by the outline, light and shade, or color of any object. Arc. See Circle. Arrangement. The orderly disposition of objects or forms. Axis of a Solid. An imaginary straight line passing through its centre and about which the different parts are symmetrically arranged. Axis of a Figure. A straight line passing through the centre of a figure, and dividing it into two equal parts. Axis of Symmetry. A straight line so placed in a solid or a plane figure that every straight line meeting it at right angles and extending in each direction to the boundary of the solid or figure is bisected at the point of meeting. In many solids and plane figures an axis of symmetry cannot be drawn. Balance. The equality of parts, obtained by the proper distribution of lines or of light and dark. Base. The opposite parallel polygons of prisms. The polygon opposite the vertex of a pyramid. The plane surfaces of cylinders and cones. The opposite parallel sides of a parallelogram or trapezoid. The shortest or longest side of an isosceles triangle, and any side in any other triangle, but usually the lowest. Bisect. To divide into two equal parts. Bisector. A line which bisects. Bisymmetrical. Having one side the exact reverse of the other side. Blend. To soften and bring together. Blocking-in Lines. The lightest and simplest suggestions of the leading lines and masses of the subject. Border. Ornament, usually composed of units regularly repeated along a line. Breadth. Simplicity due to large masses which subordinate details to the spirit and effect of the whole. Chiaro-oscuro. The art of combining light and shade.
The boundary line is called the CIRCUMFERENCE. Circumscribe. A polygon is said to be circumscribed about a circle when each side of the polygon is a tangent to the circle ; and a circle is said to be circumscribed about a polygon when the circumference of the circle passes through all the vertices of the polygon. Color. For color terms, see Color Manual. Concave. Curving inwardly. Cone. A solid bounded by a plane surface called the base, which is a circle, ellipse, or other curved figure, and by a lateral surface which is everywhere curved, and tapers to a point called the vertex. Its base names the cone. Thus a circular cone is one whose base is a circle. Concentric. Having a common Centrex. Conic Section. A section obtained by cutting a cone by a plane. Construction. The making of any object. Construction Lines. The lines by which the desired result is obtained. Constructive Drawing. A drawing intended for the workman who is to make the object. Contour. The outline of the general appearance of an object. Contour Element. An element which is in the contour of an object. Contrast. The effect due to the juxtaposition of different lines, different forms, different masses of light and dark, or different colors. Conventionalization. In art, the expression of the spirit and important truths of Nature by a subordination of less important features. Convergence. Lines extending toward a common point, or planes extending toward a common line. Convex. Rising or swelling into a spherical or rounded form. Corner. The point of meeting of the edges of a solid, or of two sides of a plane figure. Crescent. A figure.of the shape of the new moon. Cross. Two bars, or parts, intersecting or crossing each other in various ways. The symbol of the Christian religion. Cross-hatched. In mechanical drawing, a half tinting placed upon parts cut by a cutting plane. In free-hand drawing, the use of lines crossing each other and producing light and shade effects. Curvature. Variation from straightness. Curve. A line of which no part is straight.
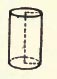
A RIGHT CIRCULAR CYLINDER is generated by the revolution of a rectangle about one side as an axis. The side about which the rectangle revolves is called the height of the cylinder, also its axis. The side opposite the axis describes the curved surface of the cylinder, and in any of its positions is called an element of the surface. Cylindrical. Having the general form of a cylinder. Degree. The 36oth part of a circumference of a circle. Describe. To make or draw a curved line. Design. Any arrangement or combination to produce desired results in industry or art. Develop. To unroll or lay out upon one plane the surface of an object
Diverging Lines. Lines extending from a common point. Edge. The intersection of any two surfaces. The boundary line. Edges are straight or curved, and are represented by lines. Elevation. A drawing made on a vertical plane by means of projecting lines perpendicular to the plane from the points of the object. The terms elevation, vertical projection, and front view all have the same meaning.
Face. One of the plane surfaces of a solid. It may be bounded by straight or curved edges. Finishing. Completing a drawing, whose lines have been determined, by erasing unnecessary lines and strengthening and accenting where this is required. Foreshortening. Apparent decrease in length, due to a position oblique (or parallel) to the visual rays. Free Arm Movement. Movement of the arm from the shoulder. Free-hand. Executed by the hand, without the aid of instruments.
Frustum. See Cone and Pyramid. Generated. Produced by. Geometric. According to geometry. Gradation. A gradual change from light to dark, or from one color to another. Half-tint. The shading produced by means of parallel equidistant lines.
Horizon. In pictorial art, a horizontal line at the level of the eye. Horizontal. Parallel to the surface of smooth water. Inscribe. A polygon is said to be inscribed in a circle when all its vertices are in the circumference of the circle ; and a circle is said to be inscribed in a polygon when the circumference of the circle is touched by each side of the polygon. Instrumental. By the use of instruments. Interlacing. The arrangement of one part of a design so that it passes alternately above and below another part. Lateral Surface. The surface of a solid excluding the base or bases. Level of the Eye. The level or position of a horizontal plane passing through the spectator's eye. Line. A line has length only. In a drawing its representation has width but is called a line.
Longitudinal. In the direction of the length of an object. Model. A form used for study. Oblique. Neither horizontal nor vertical.
Ornament. Decorative arrangement of line, light and shade, color, or relief.
Overall. The entire length.
Parallelogram. See Quadrilateral. Pattern. That which is used as a guide or copy in making anything. FLAT. One made of paper or other thin material.. Perimeter. The boundary of a closed plane figure.
Perspective. The art of making upon a plane, called the picture plane, such a representation of objects that the lines of the drawing appear to ' coincide with those of the object, when the eye is at one fixed point called the station point. Plan. Plan, horizontal projection, and top view have the same meaning, and designate the representation of an object made on a horizontal plane by means of vertical projecting lines. In architecture it means a horizontal section. Plane Figure. A part of a plane surface bounded by lines.
Polygon. A plane figure bounded by straight lines. Prism. A solid bounded by two equal parallel polygons, having their equal sides parallel, and by three or more parallelograms.
The Axis of a regular prism is a straight line connecting the centres of its bases. A RIGHT SECTION of a prism is a section made by a plane perpendicular to its lateral edges. A PARALLELOPIPED is a prism whose bases are parallelograms. Produce. To continue or extend. Profile. The contour outline of an object. Projection. Orthographic. The view or representation of an object obtained upon a plane by projecting lines perpendicular to the plane. Pyramid. A solid of which one face, called the base, is a polygon, and the other faces, called lateral faces, are triangles having a common vertex called the vertex of the pyramid. The intersections of the lateral faces are called the lateral edges. Quadrant. See Circle. Quadrilateral. A plane figure bounded by four straight lines. These lines are the sides. The angles formed by the lines are the angles, and the vertices of these angles are the vertices of the quadrilateral.
Quadrisect. To divide into four equal parts.
Radiation. Proceeding from a common point or line. Reflected Light. The light seen on the shadow side of any object, and reflected from some other object. Relation. The harmony or contrast of form, value, or color. Rendering or Handling. The way in which a medium is used. Repetition. The arrangement of a unit on a line, around a centre, about a line as axis, or upon geometric lines covering a surface. Representation. Any kind of drawing, painting, or sculpture. Retreating. Going away from. Rosette. Arrangement of petal-like units about a centre. Section. A projection upon a plane parallel to a cutting plane which intersects any object. The section generally represents the part behind the cutting plane, and represents the cut surfaces by cross-hatching. Sectional. Showing the section made by a plane. Sector and Segment. See Circle. Shadow. Shade and shadow have about the same meaning, as generally used ; but it will be well to designate by shadow those parts of an object which are turned away from the direct rays of light, while those surfaces which receive less direct rays and are intermediate in value between the light and the shadow are called shade surfaces. Similar Figures are those which have the same shape. Solid. A solid has three dimensions, length, breadth, and thickness. It may be bounded by plane surfaces, by curved surfaces, or by both plane and curved surfaces. As commonly understood, a solid is a limited portion of space filled with matter, but geometry does not consider the matter and deals simply with the shapes and sizes of solids.
Spiral. See Curve. Stippling,. Filling in the space between hatching lines, or producing an effect, by means of dots. Surface. The boundary of a solid. It has but two dimensions, length and breadth. Symbolism. The use of conventional forms to suggest ideas not inherent in the forms. Symmetry. Design. A proper adjustment or adaptation of parts to one another and to the whole. Symmetry. Geometry. If a solid can be divided by a plane into two parts such that every straight line, perpendicular to the plane and extending from the plane in each direction to the surface of the solid, is bisected by the plane, the solid is called a symmetrical solid, and the plane is called a plane of symmetry. If two planes of symmetry can be drawn in a solid, their intersection is called an axis of symmetry. See Axis of Symmetry. Technique. The handling or way in which an effect is obtained. Texture. The character of a surface.
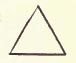
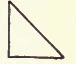
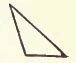
Triangle. A plane figure bounded by three straight lines. These lines are called the sides. The angles that they form are called the angles of the triangle, and the vertices of these angles, the vertices of the triangle.
An EQUIANGULAR TRIANGLE is one in which the three angles are equal. The value of each angle is 6o°. The BASE is the side on which the triangle is supposed to stand. In an isosceles triangle, the equal sides are called the legs, the other side the base; in other triangles any one of the sides may be called the base. The ALTITUDE is the perpendicular distance from the vertex to the base. Except in the isosceles triangle, there are three altitudes. The vertex of the angle opposite the base is often called the vertex of idle- triangle. Trisect. To divide into three equal parts. Truncated. A truncated solid is the part of a solid included between the base and a plane cutting the solid oblique to the base. Type Form. A perfect geometrical plane figure or solid. Unit of Design. The figure repeated in a design or arrangement. Value. In color the relative amount of light contained in different colors. The strongest value is the lightest. Variety. The effect due to the combination of parts which are not alike.
Vertex. See Angle, Quadrilateral, Triangle. The vertex of a solid is the point in which its axis intersects the lateral surface. View. See Elevation. Views are called front, top, right or left side, back, or bottom, according as they are made on the different planes of projection. They are also sometimes named according to the part of the object shown, as edge view, end view, or face view. Working Drawing. One which gives all the information necessary to enable the workman to construct the object. Working Lines. See Lines. The End. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Online Art Books
Freehand Drawing Book ArtGraphica |



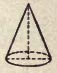 A RIGHT CIRCULAR CONE is generated by an isosceles triangle which revolves about its altitude as an axis. The equal sides or the triangle in any position are called elements of the surface. The length of an element is called the slant height of the cone. Unless otherwise stated " cone " means a right circular cone.
A RIGHT CIRCULAR CONE is generated by an isosceles triangle which revolves about its altitude as an axis. The equal sides or the triangle in any position are called elements of the surface. The length of an element is called the slant height of the cone. Unless otherwise stated " cone " means a right circular cone.

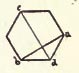 Diagonal. A straight line in any polygon which connects vertices not adjacent.
Diagonal. A straight line in any polygon which connects vertices not adjacent. Diameter. See Circle. In a regular polygon with an even number of sides a line joining the centres of two opposite sides is often called a diameter.
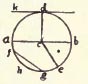
Diameter. See Circle. In a regular polygon with an even number of sides a line joining the centres of two opposite sides is often called a diameter.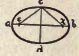 Ellipse. A plane figure bounded by a line such that the sum of the distances of any point in it, as c, from two given points e and f, called foci, is equal to a given line, as a b. The point midway between the foci is called the centre.
Ellipse. A plane figure bounded by a line such that the sum of the distances of any point in it, as c, from two given points e and f, called foci, is equal to a given line, as a b. The point midway between the foci is called the centre. Fret. A band or border composed of lines forming a succession of angles and often interlacing.
Fret. A band or border composed of lines forming a succession of angles and often interlacing. Hemisphere. Half a sphere, obtained by bisecting a sphere by a plane.
Hemisphere. Half a sphere, obtained by bisecting a sphere by a plane. Oblong. A rectangle with unequal sides.
Oblong. A rectangle with unequal sides.

 Parallel. Having the same direction and everywhere equally distant.
Parallel. Having the same direction and everywhere equally distant. Perpendicular. At an angle of 90°.
Perpendicular. At an angle of 90°. Plinth. A cylinder or prism, whose axis is its least dimension. It is circular, triangular, square, etc., according as it has circles, triangles, squares, etc., for bases.
Plinth. A cylinder or prism, whose axis is its least dimension. It is circular, triangular, square, etc., according as it has circles, triangles, squares, etc., for bases.

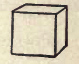 2. The HEXAHEDRON, or CUBE, which has six square faces.
2. The HEXAHEDRON, or CUBE, which has six square faces.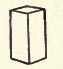
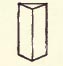
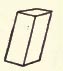
 A pyramid is called triangular, square, etc., according as its base is a triangle, square, etc.
A pyramid is called triangular, square, etc., according as its base is a triangle, square, etc.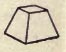 A FRUSTUM of a pyramid is the part included between the base and a plane parallel to the base and cutting all the lateral edges.
A FRUSTUM of a pyramid is the part included between the base and a plane parallel to the base and cutting all the lateral edges. A TRUNCATED PYRAMID is the part included between the base and a plane oblique to the base and cutting all the lateral edges.
A TRUNCATED PYRAMID is the part included between the base and a plane oblique to the base and cutting all the lateral edges.
 Quatrefoil. A figure composed of four leaf-like parts.
Quatrefoil. A figure composed of four leaf-like parts. Sphere. A solid bounded by a curved surface every point of which is equally distant from a point within called the centre.
Sphere. A solid bounded by a curved surface every point of which is equally distant from a point within called the centre. Spheroid (Ellipsoid). A solid generated by the revolution of an ellipse about either diameter. When revolved about the long diameter, the spheroid is called prolate or the long spheroid ; when about the short diameter, it is called oblate or the flat spheroid. • The earth is an oblate spheroid.
Spheroid (Ellipsoid). A solid generated by the revolution of an ellipse about either diameter. When revolved about the long diameter, the spheroid is called prolate or the long spheroid ; when about the short diameter, it is called oblate or the flat spheroid. • The earth is an oblate spheroid. Trefoil. A figure composed of three leaf-like parts.
Trefoil. A figure composed of three leaf-like parts.

 Vertical. Upright or perpendicular to a horizontal plane or line. Vertical and perpendicular are not synonymous terms.
Vertical. Upright or perpendicular to a horizontal plane or line. Vertical and perpendicular are not synonymous terms.






