Theory of Perspective |
||||||||||||||||
|
Page 02 / 25
THE PRACTICE AND THEORY OF PERSPECTIVE AS APPLIED TO ART
 PART I NATURE'S PERSPECTIVE AS SEEN AND USED DAILY BY PAINTERSCHAPTER I : THE PRINCIPLE OF PERSPECTIVE IN THEORY"If you do not rest on the good foundation of nature, you will labour with little honour and less profit."—LEONARDO DA VINCI. LINEAR Perspective is a study that deals with the appearance of objects[1] as regards their size and the direction of their lines seen at varying distances and from any point of view. When practising it we are not concerned with their apparent changes of colour or tone, though those also help us to recognise the distance separating us, or that of one object from another. Visual rays. — The Theory of Perspective is based on the fact that from every point of an object that we are looking at, a ray of light is carried in a straight line to our eye[2] By these innumerable rays we gain the impression of that object (Fig. 1). 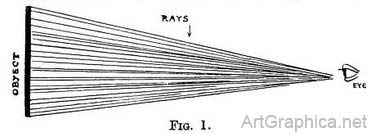
1 " Objects " is a mean word to use, because perspective laws also apply to the surface of the earth, the sea, and the sky, and all living things. It is used for convenience. 2 We see objects at a different angle according to whether we have both eyes open, the left shut, or the right shut. When drawing objects very close at hand look with one eye only. Tracing on glass. — If we look at an object through a sheet of glass we can trace on that glass the apparent height or width of that object (Fig. 2) ; in other words, we can mark off on the glass those points where the rays from the extremities of the object on the way to our eye pass through it. 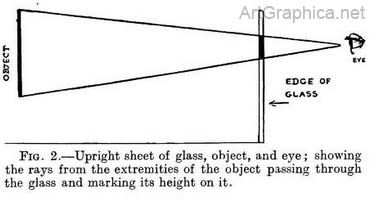
Fig 2. Upright sheet of glass, object, and eye; showing the rays from the extremities of the object passing through the glass and marking its height on it. Height of objects at varying distances traced on glass. — If we now place two objects of similar height one behind the other (Fig. 3) our tracing of each discovers the one farthest off to appear on the glass shorter than the one close at hand. Fig. 3 makes it evident that this apparent difference in size is due to the fact that the converging rays from the further object have the longest distance to travel, and so are nearly together where they pass through the glass. On the other hand, the rays from the object close to the glass have only just started on their journey and so are still wide apart. 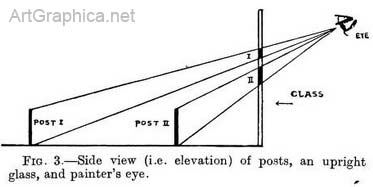
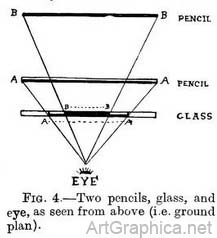
Width of objects traced. — Let us repeat the experiment with two pencils of equal length lying on a fiat surface, one behind the other. We shall, be satisfied that their apparent length, as traced on the glass (Fig. 4), is also determined by these rays, and that the near one looks longer than the distant one. We have seen that the height and width of objects as they appear to us is determined by the converging rays from their extremities to our eye ; that objects really equal in size appear shorter and narrower when further away.
Fig. 5 represents three pinheads in a row, one behind the other, on the far side of the glass from the position of the eye. Notice, however, that the eye is above the pins (i.e. looking down on them), and so the points where their rays cut the glass are one above the other in regular order, the nearest pin (3) appearing the lowest down on the glass. 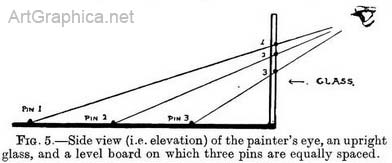
Since the pins were placed at equal distances apart, their spacing, as shown on the glass, would also fix the depths of the ground surface between them:(Fig. 6). 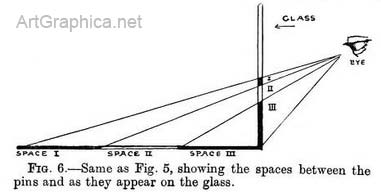
Theory of tracing applied to measurements on a canvas. — Up to now we have supposed ourselves tracing objects through a sheet of glass. In a perspective drawing our canvas is supposed to be a glass, and on it we trace only those objects that we can see through it without moving our heads. But painters should be practical ; so set up a canvas and prove to yourself that objects of equal size when far off appear narrower, shorter, and less deep than the near ones, and that the spaces between them undergo a corresponding reduction. To do this, follow the instructions in Figs. 9 and 11. 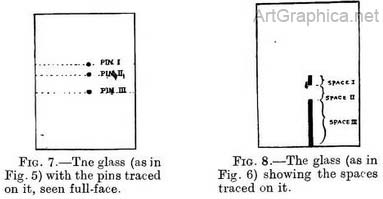
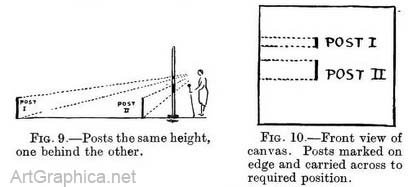
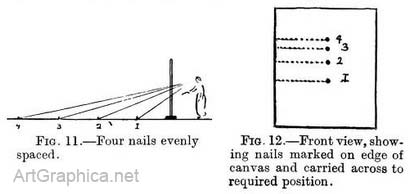
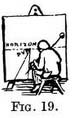
Fig. 9. Be yourself the " Painter." See that your canvas is vertical and so placed that the posts are just visible at one edge. With one eye shut and head still, mark off the heights of the posts where they seem to touch the canvas.
Theory of tracing to explain why parallel receding lines appear to meet. — Some people, when looking down a long straight length of railway track, have been curious to understand why the lines appear to get narrower and finally to meet in the far distance, though they know that the lines are actually parallel. It can be explained by tracing in this way—Fig. 14 shows that a piece of the railway line on the glass would appear as an upright line, the near end of the line being the lowest on the glass. 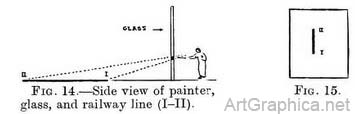
The tracing on the glass would look like this (Fig. 15). Fig. 16 shows how wide the near and far part of the track respectively would look on the glass, so that a front view of the glass (Fig. 17) would be like this. 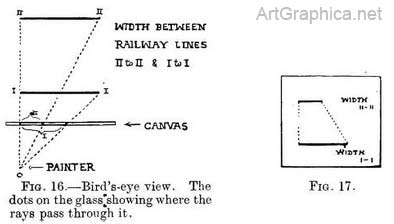
(In Fig. 14 we proved that the far end of the rail appeared higher up on the glass than the near end.)
The trace of a level receding surface seen from below. — In former Objects exercises we have had our eye higher than the objects we traced (so that we looked down on them) and the near objects became the lowest on the glass; as in Figs. 4 and 5. The reverse happens when our eye is lower than the object (Fig. 20). 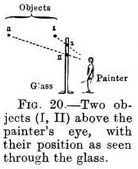
AN EXPLANATION OF TERMS USED IN PERSPECTIVETHE HORIZON
When standing or sitting on flat land the surface between us and the distant horizon is so foreshortened that mere hedges and bushes may hide miles of country and blot out the horizon. From a hill-top we look down upon the flat land, and the former narrow strip between us and the horizon looks deeper ; also from this height we see more distant land.
If the sea forms the boundary of our view the tips only of ship's masts may be seen beyond the apparent meeting of sky and sea. This explains that the curvature of the earth between us and the horizon is a real consideration for the landscape and sea painter, and it provides a reason for our seeing more distance from a height than from a slight rise. The horizon on our picture. — Though the horizon in Nature is a curved line, it is usual in pictures to represent it as perfectly level and straight ; the reason being that we can only see a small stretch of so large a circle at one time without moving our heads (Fig. 23). 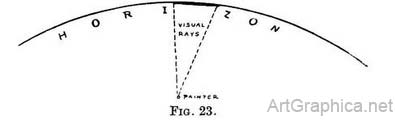
We draw this level line of the horizon straight across our picture. It is a matter of artistic taste and judgment whether we place it low, high, or in the centre of our canvas. It is essential, however, to understand that the position of the horizon line in relation to all the objects in our picture affords evidence of how high up we ourselves were when painting the scene. For instance, if we stand while we paint a whole length figure (on level ground) the horizon line would be cut by the head of our portrait (Fig. 24). When you are painting an actual scene, you will draw the horizon line, whether it is visible or not in Nature, on your picture as soon as you have decided on the size of the principal objects. The horizon in Nature will be at the exact height of your eye, i.e. at that height where neither the upper nor lower surface of a level board (but only its near edge) would be visible.
If our model is standing on a throne and we sit to paint on a low stool, our horizon is about the level of his feet. Out of doors a slight rise on otherwise level ground would present a similar effect (see Illus. I). In a room we can find the horizon by measuring the height of our eye from the ground and chalk-marking that height on the wall facing us. Out of doors on hilly ground a stick with the height of our eye marked on it can be stuck in the ground just in front of us ; where that mark cuts the view will be the horizon. Note. — Michael Angelo de Carravaggio in his picture, " Christ carried to the tomb," used so low a horizon that no space of ground is seen between the standing figures, their feet being all on a horizontal line. Rubens painted his " Henry IV setting out for the war in Germany " with the spectator's eye level with the waist of the figures ; thus making the figures important though they occupy only half the height of the canvas, and leave room for the full height of the columns and archways overhead. Leonardo da Vinci conceived his picture, " The Virgin, Saint Anne, and the Infant Jesus," as though the spectator's eye was at the level of the seated figure ; but he chose to place the latter high up on the canvas. In this way the horizon, though a low one, is actually three-quarters of the way up the canvas. These examples should clear up any confusion in regard to the position of the horizon (representing the height of the spectator's eye) in the scene to be painted, and its position on the canvas. THE PRINCIPAL VANISHING POINT (" P.V.P.")

Illus. III. Van Eyck (Photo Mansel.) - La Vierge au Donateur The horizon (as shown by the distant view) passes behind the heads of the figures. The painter must also have been sitting, because if he had been standing his horizon would have been above their heads (see Chap. II). The lines of the pavements, capitals, and plinth of the columns all tend towards one spot on the horizon at its centre. For explanation of this, see Rules I, II, Chap. II. To obtain the deptlalof each tile, see end of Chap. II. The drawing of their pattern is explained in Chap. XVI. A good example of this is seen in the line of the central row of the pavement in Van Eyck's picture (Illus. III).
From this picture we know that the painter stood at his work, and looked straight down the line marked X. THE STATION POINT AND LINE OF SIGHTThe term Station Point is used to designate that place where the painter stood or was supposed to stand (Fig. 29). 
If you sat astride a very long straight level wall looking down it, then the far end of the wall would seem to end at the P.V.P., and the spot you sat on would be the " station point," while the length between these would be the " line of sight " (Figs. 31 and 31A). This being so, we will in future call the station point " Painter." 1 It is so placed in Van Eyck's picture just mentioned. The painter was over the central row of tiles, immediately facing the central arch (Illus. III).
VANISHING POINTSThe P.V.P. is, as we have said, on the horizon and directly facing us. All level receding lines that are in Nature at right angles to the front of our face (i.e. parallel to our " line of sight ") seem to steer to that P.V.P. (Illus. IV) as will be explained in Chap. II. But there are level lines in Nature placed at other angles than this, and they tend to other spots on the horizon (Illus. V). Each level line (or set of parallel lines) has its own V.P. to which it runs. Besides these level lines there are others on inclined planes that run to vanishing points above or below the horizon, according to their position. Some of these level receding lines will be at such an angle that the points they run to will be further to the left or right than the width of ground we propose to paint, and consequently will be outside the extremities of our picture as V.P.--- in Fig. 32). As for some of the inclined planes, the lines of these will sometimes tend to points far above or below that portion of the ground or sky we wish to include in our picture. In practice we may draw the scene on a small scale in the middle of a large sheet of paper so as to have room for these outside V.P.'s on the margin. Then we can " square up " (see Note 1 in Appendix) the little picture and enlarge it on the selected canvas. Another way is to use the floor as an extension of your canvas. 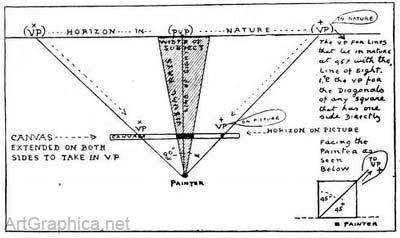 THE THEORY OF PERSPECTIVE EXPLAINED BY A DIAGRAM Fig. 32.—A bird's-eye view of the horizon, canvas, painter, and three vanishing points in Nature and on the canvas. It will be seen from this diagram that the distance along the horizon in Nature, from the P.V.P. to the V.P. for the diagonals of a square, is the same, as from the P.V.P. to " painter " ; consequently (as the diagram proves) the distance along the horizon on the picture, from P.V.P. to V.P. for diagonals, is the same as from P.V.P. to " painter." From this we learn that the V.P. for the diagonals of a square (provided that one side of the square is parallel to the horizon) is the same distance from the P.V.P. as the painter is from his canvas.
Next Page
Rules of Perspective Prev Page Perspective for Artists
|
||||||||||||||||
 Depths of objects on a level surface traced. — It only remains to find out that the depths on a receding surface are governed by the same laws.
Depths of objects on a level surface traced. — It only remains to find out that the depths on a receding surface are governed by the same laws. Fig. 11. Behave as in the last exercise ; tick off the position of each nail on the edge of the canvas.
These nails might represent the cracks between floorboards, and our drawing shows that each board would appear one above the other (Fig. 13), necessarily narrower from No. 1 the nearest to 4 the farthest away.
Fig. 11. Behave as in the last exercise ; tick off the position of each nail on the edge of the canvas.
These nails might represent the cracks between floorboards, and our drawing shows that each board would appear one above the other (Fig. 13), necessarily narrower from No. 1 the nearest to 4 the farthest away.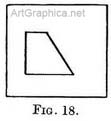
 As we have secured the width of a piece of the track at its near and far end, we can join the ends on each side to make the rails. The tracing on the glass (Fig. 18) shows the rails getting closer and closer as they recede, and we see that they would, if longer, appear to meet. The spot on the glass where the receding lines appear to end (or meet) is at the same level as your eye (Fig. 19).
As we have secured the width of a piece of the track at its near and far end, we can join the ends on each side to make the rails. The tracing on the glass (Fig. 18) shows the rails getting closer and closer as they recede, and we see that they would, if longer, appear to meet. The spot on the glass where the receding lines appear to end (or meet) is at the same level as your eye (Fig. 19).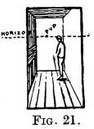 Let us again draw our piece of railroad as in Fig. 18, it will serve as the floor of a room. Above it we can draw the ceiling if we still follow out Fig. 4, but remember to make the far end below the near end, as explained in Fig. 20. Our drawing (Fig. 21) shows that if we look down on level surfaces their receding lines must be drawn no.xo running up the canvas (from their near end to their far end). On the other hand, if we see their under side the lines must be made to run down the canvas as they recede.
Let us again draw our piece of railroad as in Fig. 18, it will serve as the floor of a room. Above it we can draw the ceiling if we still follow out Fig. 4, but remember to make the far end below the near end, as explained in Fig. 20. Our drawing (Fig. 21) shows that if we look down on level surfaces their receding lines must be drawn no.xo running up the canvas (from their near end to their far end). On the other hand, if we see their under side the lines must be made to run down the canvas as they recede. The visible horizon in Nature is that immense and distant circle that appears to be the extremity of our globe. Perched on a masthead we could, by moving round, examine the far distance where the sky and sea seem to meet, until piece by piece the whole circumference had come under our scrutiny (Fig. 22). On land we rarely get anything but an interrupted view of a portion of the horizon.
The visible horizon in Nature is that immense and distant circle that appears to be the extremity of our globe. Perched on a masthead we could, by moving round, examine the far distance where the sky and sea seem to meet, until piece by piece the whole circumference had come under our scrutiny (Fig. 22). On land we rarely get anything but an interrupted view of a portion of the horizon.

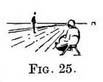 But if we sit to paint him then the horizon line will pass through his waist (Fig. 25), and we should get a more foreshortened view of the floor. It would be an absurd proceeding to begin a painting of an imaginary scene without first fixing the place where you suppose yourself to be painting it from. The relative position of the horizon line and the principal figures or other objects size be decided on at the onset ; after that the locality and size of all additional objects will be governed by the horizon.
But if we sit to paint him then the horizon line will pass through his waist (Fig. 25), and we should get a more foreshortened view of the floor. It would be an absurd proceeding to begin a painting of an imaginary scene without first fixing the place where you suppose yourself to be painting it from. The relative position of the horizon line and the principal figures or other objects size be decided on at the onset ; after that the locality and size of all additional objects will be governed by the horizon.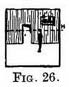
 We may consider the horizon as a distant imaginary line parallel to the front of our face and stretching across the view at the actual height that our eye is from the ground[1] (Illus. II, III) ; so if standing in a room our horizon would be roughly 5 ft. 6 in. from the floor (Fig. 26), or if we are sitting 3 ft. 6 in. (Fig. 27).
We may consider the horizon as a distant imaginary line parallel to the front of our face and stretching across the view at the actual height that our eye is from the ground[1] (Illus. II, III) ; so if standing in a room our horizon would be roughly 5 ft. 6 in. from the floor (Fig. 26), or if we are sitting 3 ft. 6 in. (Fig. 27).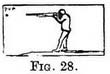 If you were to look down the barrel of a gun, holding it quite level (Fig. 28), the point you aimed at would in Perspective be called the Principal Vanishing Point (P.V.P.), and it would be on that imagined line that represents the horizon. It is the spot that a level line running directly away from us tends to.
If you were to look down the barrel of a gun, holding it quite level (Fig. 28), the point you aimed at would in Perspective be called the Principal Vanishing Point (P.V.P.), and it would be on that imagined line that represents the horizon. It is the spot that a level line running directly away from us tends to. 1. " From the ground," more correctly " from the sea-level " ; because if we went up a mountain to see the view, the horizon would still be on a line with our eye, so it would be the height of our; eye plus the mountain, illustration III makes this clear.
1. " From the ground," more correctly " from the sea-level " ; because if we went up a mountain to see the view, the horizon would still be on a line with our eye, so it would be the height of our; eye plus the mountain, illustration III makes this clear. In a composed picture we can place the P.V.P. where we like on the horizon, but we must remember that it represents the point immediately in front of us (Fig. 29) that we were supposed to be looking at. Theoretically it is half-way between one side of our picture and the other[1], but this need not hamper us.
In a composed picture we can place the P.V.P. where we like on the horizon, but we must remember that it represents the point immediately in front of us (Fig. 29) that we were supposed to be looking at. Theoretically it is half-way between one side of our picture and the other[1], but this need not hamper us.
 If you see on a picture the representation of what was in Nature a level receding line, drawn as a vertical line, then you will know that the far end of it points to the P.V.P. on the horizon, and that the painter was straight in front of that spot and looking at it (Fig. 30).
If you see on a picture the representation of what was in Nature a level receding line, drawn as a vertical line, then you will know that the far end of it points to the P.V.P. on the horizon, and that the painter was straight in front of that spot and looking at it (Fig. 30).









