Drawing Depth |
||||||||||||||||
|
Page 04 / 25
 CHAPTER III DEPTHSTWO very practical ways for finding depths on a receding surface are (A) by the use of diagonal lines with a receding scale ; (B) by a scale on the base-line or parallel to it. The former in particular is useful when sketching a foreshortened row of posts, trees, etc., for it marks the distance between each with sufficient accuracy, and all the lines can be drawn rapidly freehand. (A) Depths found by diagonals and a receding scale. — The construction of a gate may include two uprights, some rails, and one or more cross-bars (Fig>c. 51). The centre is at the meeting of the cross-bars. 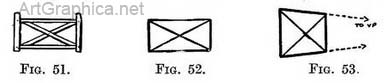
Therefore to find the centre of a gate or any other rectangular form we draw diagonal lines from corner to corner (Fig. 52). This applies equally well to any rectangular shape seen foreshortened (Fig. 53). If we add an upright where the diagonals meet (Fig. 54) we divide the form into two halves, of which the nearer appears to be the larger. Suppose you had a gate with one-cross bar (Fig. 55) and wished to add another half of a gate to its length, then (remembering that the diagonal line determined the centre) you could utilise half the existing gate for a new diagonal. This would start at the junction of the central upright and the top rail (Fig. 56) and would pass through the middle of the end upright, meeting the new bottom rail where the new upright is to come (Fig. 57). 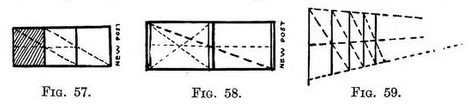
By the use of two diagonals you might also fix the meeting-place for the new upright with the top rail, but this is unnecessary. If you would like to add a whole gate to another, instead of half at a time (as we did), then continue the three bars and make a new diagonal (Fig. 58) from the top corner of one end-post and pass it through the centre of the other end-post. Where it touches the bottom rail make the new post. 
Our essay on the construction receding row of posts or trees. Proceed thus (Fig. 59) : Draw post 1. Fix height and centre of future posts by lines receding to V.P. from top, bottom, and middle of post 1. Draw post 2. From top of post 1 take a diagonal through centre of post 2—where it touches receding line on ground plant post 3. Carry on by drawing another diagonal from the top of post 3 and each post as it is erected.
Our vertical scale will do equally well for level surfaces (Fig. 61) ; or we can make it on the ground (Fig. 62). If Fig. 59 is looked at from the side it will lie flat and be similar to Fig. 62 Many examples of the use of diagonal lines in conjunction with the receding scale will crop up as we get on with our subject. These should be enough to explain the principle. But I wanted to make it clear that receding lines in perspective not only form a scale for measuring heights and widths, but with the addition of the diagonal line give the depth measurement. 
1. Turner delighted in the regnlarity of these receding spaces. His pictures show this not only in the architecture that he drew so beautifully, but also in his choice of subjects where trees line a roadway. He knew just where to break the monotony of too even a distribution without disturbing the feeling of sequence given by an avenue. One calls to mind his embankment on the Seine ("Rivers of France") and " Mortlake Terrace—Summer Evening."
The foreshortened line is more often the one we have to divide into certain proportions as in Fig. 64, line 1-2. To do so, take a line from the near end 1 to the horizon line, thus making a V.P. From the V.P. take a line to the far end 2, continuing it sufficiently far to enable the line 1-3 to be drawn horizontally. Line 1-3 now represents the foreshortened line seen full-face. Divide 1-3 into required proportions, and from each division take lines to the V.P. They will divide line 1-2 into like proportions. 
The divisions marked on the full-face line might represent the ground plan of the length of a colonnade with the spaces between the columns ; then the same divisions would on the foreshortened line be the perspective ground plan of their width. On these the columns would be raised (Fig. 66). ANOTHER WAY OF USING DIAGONAL LINES TO FIND DEPTHS
The above Figs. 67-69 can be worked equally well with a " downhill " V.P. In some cases this may be more convenient. The diagonal of the first space must of course be taken from the top near corner to the " downhill " V.P. (immediately under the V.P. for the level lines). The depths of succeeding spaces will be fixed at those points where the diagonals cut the bottom receding line.
In Fig. 74 we see that the diagonals taken to the bottom line and those taken to the new line both pass through the top receding line at the same points. 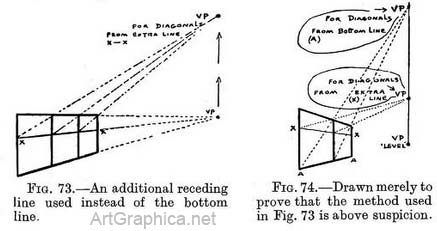
Diagonal V.P. on inclined planes. — A space that would be level as we walk across it from one side to the other (A to B, Fig. 76A) but uphill (or downhill B to C) as we walk from the near-end to the far end must have its V.P. for the diagonal at the same level as the P.V.P. to which their sides tend.
1. Measure it with your pencil held vertically at arm's length. When the length of pencil between its top and your thumbnail covers the depth of the square exactly, rotate the pencil until it lies along the near edge of the square to see how many times the depth would go into the length. I believe this is the only way of making sure that the square .form shall look as you would wish it to be, and to avoid those distorted representations that disfigure too many books on Perspective, and occasionally some pictures. The depth of many squares. — With one square drawn and its diagonal continued to find the V.P. we can find the depth of any other square wherever we wish it to be (Fig. 77B). We do so by first drawing the near-edge parallel to that of the first square. Its length we determine by using the receding lines of the first square as a scale. The sides of the new square will recede to the P.V.P. (Rule I), and we shall fix its depth at the point where the diagonal crosses one of the receding lines. 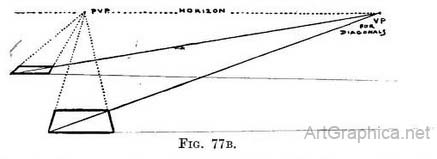
One diagonal to find depths. — By the use of one diagonal line we can find the depth of any number of rectangular spaces provided they are (in Nature) of equal dimensions (Figs. 78-81). 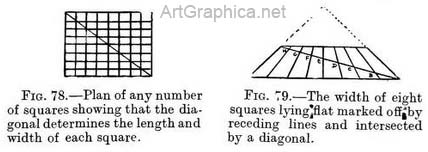 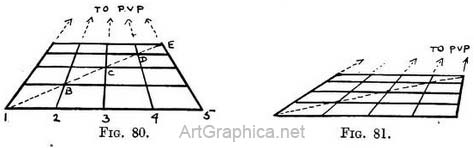
Procedure. — Draw a line (1-5,[1] Fig. 80) parallel 'to horizon line. On it mark off the width of the divisions required. From each division (1, 2, 3, 4, 5) draw lines meeting at P.V.P. These fix the width of each space. Draw a diagonal. At the points (B, C, D, E, etc.) where the diagonal cuts the receding lines (1, 2, 3, 4, 5) draw lines parallel to line 1-5, and so obtain the depth of each row of spaces. The position of vanishing point for diagonals (D.V.P.) is determined by the distance the painter is from his picture or from the object he paints. I have advised you to place a square lying level with one side facing you in the foreground of the scene you intend to paint, and to copy its depth in relation to some principal object ; this done, to draw its diagonal and continue it to the horizon to find the V.P. for diagonals D.V.P. Most painters prefer to fix this D.V.P. for diagonals first. In order to do so, you must decide at what distance you wish your finished picture to be seen.
The actual distance from the D.V.P. (the vanishing point for diagonals) measured along the horizon line on your picture to the P.V.P., will be the same as the 6 measured distance along the ground from " painter " (i.e. the place you suppose yourself to be while painting) to the P.V.P. on the picture a general rule, you consider that your picture should be viewed at a distance equal to twice its height or length—whichever is greatest—so that the whole picture may be seen clearly and yet without moving the head—but we will talk of this later on. See Appendix, Note 3, for methods of dividing a line. Fig. 83 represents the picture (3 ft. square) shown on the ground plan in Fig. 82. The V.P. for diagonals is 6 ft. from the P.V.P., just as the painter was 6 ft. from the picture. 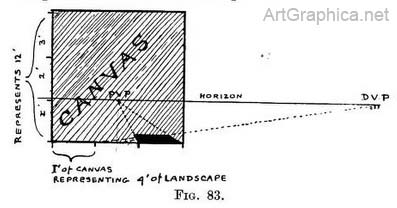
Vanishing point for diagonals can be used above or below the horizon.— As all lines which are in Nature level and at an angle of 45° with the line of sight tend to the D.V.P. on the horizon, so also lines leaning upwards or downwards tend to a D.V.P. respectively above or below the horizon, provided they make an angle of 45° with level ground surface. The " uphill " or " downhill " D.V.P. will respectively be just as far above or below the horizon as the D.V.P. on it is from the P.V.P., as in Fig. 84.
Next Page
Foreshortening Drawing Prev Page Rules of Perspective
|
||||||||||||||||
 Applied to a colonnade, etc. — When sketching an avenue of evenly-spaced trees or a colonnade make a receding scale of three lines, as in Fig. 59—it would be most inconvenient to take in the tops of the trees (Fig. 60).[1]
Applied to a colonnade, etc. — When sketching an avenue of evenly-spaced trees or a colonnade make a receding scale of three lines, as in Fig. 59—it would be most inconvenient to take in the tops of the trees (Fig. 60).[1]
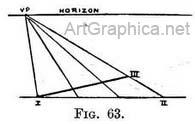 (B) Depths found by a scale on the base-line. — If (Fig. 63) we saw a line (I-II) full-face, it being divided into equal proportions, and we carried receding lines from both ends (I-II) and from each division to a V.P. on the horizon; then a foreshortened line (I-III) would also be divided into similar proportions in perspective ; each division getting regularly shorter from the nearest to the farthest end of the line.
(B) Depths found by a scale on the base-line. — If (Fig. 63) we saw a line (I-II) full-face, it being divided into equal proportions, and we carried receding lines from both ends (I-II) and from each division to a V.P. on the horizon; then a foreshortened line (I-III) would also be divided into similar proportions in perspective ; each division getting regularly shorter from the nearest to the farthest end of the line.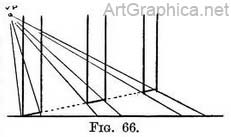 The division of a receding line into equal or spaces - Unequal divisions are obtained in
a similar way (as in Fig. 65).
The division of a receding line into equal or spaces - Unequal divisions are obtained in
a similar way (as in Fig. 65).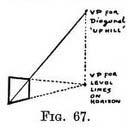 (1) Of vertical spaces. — Fig. 67 represents a foreshortened rectangular form (say a window) in an upright position. If we draw a diagonal from the near bottom corner to the far top corner, then that diagonal is a receding line I inclined upwards, and its vanishing point will be found by continuing its course until it meets a vertical line that starts from V.P. 1.
(1) Of vertical spaces. — Fig. 67 represents a foreshortened rectangular form (say a window) in an upright position. If we draw a diagonal from the near bottom corner to the far top corner, then that diagonal is a receding line I inclined upwards, and its vanishing point will be found by continuing its course until it meets a vertical line that starts from V.P. 1.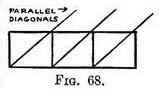 (Rule III says that a line inclining upwards tends to a V.P. immediately above the point it would tend to if it were a level line.) It is evident (Fig. 68) that the diagonals of any number of shapes equally proportioned would in Nature be parallel lines, and therefore when seen receding (Rule I) would meet at the same point, as in Figs. 69 and 70.
(Rule III says that a line inclining upwards tends to a V.P. immediately above the point it would tend to if it were a level line.) It is evident (Fig. 68) that the diagonals of any number of shapes equally proportioned would in Nature be parallel lines, and therefore when seen receding (Rule I) would meet at the same point, as in Figs. 69 and 70.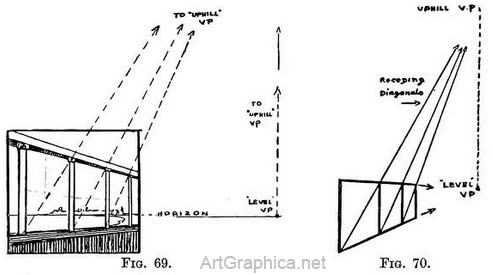 In order to find the apparent depths of equally proportioned a receding row we must find the " uphill " V.P. for the first space, and from that V.P. draw perspective diagonals to the far bottom corner of each space as it is made. The intersection of the diagonals with the top receding line will mark the depth for each succeeding space.
In order to find the apparent depths of equally proportioned a receding row we must find the " uphill " V.P. for the first space, and from that V.P. draw perspective diagonals to the far bottom corner of each space as it is made. The intersection of the diagonals with the top receding line will mark the depth for each succeeding space.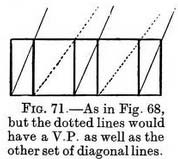
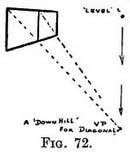 If you find the V.P.'s for inclined lines come inconveniently high or low you can take an extra receding line to the level V.P., so as to cut off a portion of the height of the first spaced and others to come. Use that new line to run the diagonals to, instead of the top line (if an " uphill " V.P. is being used) or bottom line (for a " downhill " V.P.). Fig. 73.
If you find the V.P.'s for inclined lines come inconveniently high or low you can take an extra receding line to the level V.P., so as to cut off a portion of the height of the first spaced and others to come. Use that new line to run the diagonals to, instead of the top line (if an " uphill " V.P. is being used) or bottom line (for a " downhill " V.P.). Fig. 73.
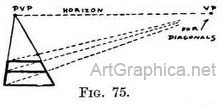 (2) Of level spaces. — Our examples (Figs. 67-72) have been of vertical spaces. The depth of spaces on level ground are found in a similar way. No further explanation is necessary than what Fig. 75 affords.
(2) Of level spaces. — Our examples (Figs. 67-72) have been of vertical spaces. The depth of spaces on level ground are found in a similar way. No further explanation is necessary than what Fig. 75 affords.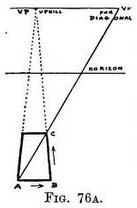 On an inclined and tilted plane. - But if that space was on a surface not only inclined upwards, but also tilted from one side to the other (A to B, Fig. 76B), then the V.P. for its diagonal would be on a line from the " uphill " V.P., and that line would run parallel to A–B. These explanations could
have been expressed thus : " The V.P. for the diagonal is in the same plane as the surface the diagonal crosses," but such a concise remark might leave some readers still thinking.
On an inclined and tilted plane. - But if that space was on a surface not only inclined upwards, but also tilted from one side to the other (A to B, Fig. 76B), then the V.P. for its diagonal would be on a line from the " uphill " V.P., and that line would run parallel to A–B. These explanations could
have been expressed thus : " The V.P. for the diagonal is in the same plane as the surface the diagonal crosses," but such a concise remark might leave some readers still thinking.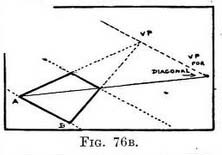 The depth of a square. — It is of supreme importance in every picture that the depth of some foreshortened space should be drawn with absolute accuracy. It matters little whether it is an upright space or one on the ground, but we must have one space as a correct guide for obtaining all other depths. Suppose you have to draw a number of squares (such as the tiles of a pavement) whose sides tend to the P.V.P. If the pavement is in front of you then you can copy exactly[1] how deep one tile should be compared with its length ; but be sure you place it correctly in the floor-space or your labour is wasted.
The depth of a square. — It is of supreme importance in every picture that the depth of some foreshortened space should be drawn with absolute accuracy. It matters little whether it is an upright space or one on the ground, but we must have one space as a correct guide for obtaining all other depths. Suppose you have to draw a number of squares (such as the tiles of a pavement) whose sides tend to the P.V.P. If the pavement is in front of you then you can copy exactly[1] how deep one tile should be compared with its length ; but be sure you place it correctly in the floor-space or your labour is wasted.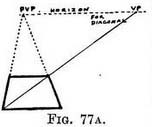 The diagonal you draw through that tile (Fig. 77A) fixes the V.P. for the diagonals of every other tile in the pavement. In other words, the receding diagonals from that V.P. determine the depth of any and every level square on the ground or above it, if one of their edges is parallel to the picture plane (usually the uprightsquares can be worked from this one also, as explained by Fig. 61). If your picture is composed and you have no actual sqUare in front of you, I advise you to cut out a square of cardboard, place it at the actual distance you wish it to be in the scene, and draw its proportions.
The diagonal you draw through that tile (Fig. 77A) fixes the V.P. for the diagonals of every other tile in the pavement. In other words, the receding diagonals from that V.P. determine the depth of any and every level square on the ground or above it, if one of their edges is parallel to the picture plane (usually the uprightsquares can be worked from this one also, as explained by Fig. 61). If your picture is composed and you have no actual sqUare in front of you, I advise you to cut out a square of cardboard, place it at the actual distance you wish it to be in the scene, and draw its proportions.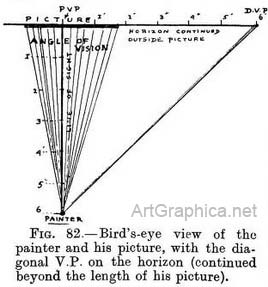 If you wish the owner to examine it at close quarters, you will suppose yourself to be just that short distance as he would be from PvP DV it, while you paint. If it is to be seen far away, you suppose yourself to be far off also when painting it.
If you wish the owner to examine it at close quarters, you will suppose yourself to be just that short distance as he would be from PvP DV it, while you paint. If it is to be seen far away, you suppose yourself to be far off also when painting it.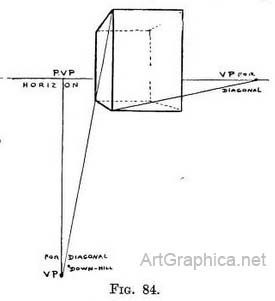 If each foot length along the bottom edge (base line) of the picture represents 4 ft. of the nearest width of the scene painted, then the actual length of the nearest foreground represented is 12 ft. The oblong drawn on the picture was 4 ft. long and 8 ft. deep, and was 2 ft. to the right of the painter's `line of sight. Similarly the same scale of 4 ft. of Nature 1 ft. of canvas shows that the painter's eye (the horizon) was 4 ft. above the ground level.
If each foot length along the bottom edge (base line) of the picture represents 4 ft. of the nearest width of the scene painted, then the actual length of the nearest foreground represented is 12 ft. The oblong drawn on the picture was 4 ft. long and 8 ft. deep, and was 2 ft. to the right of the painter's `line of sight. Similarly the same scale of 4 ft. of Nature 1 ft. of canvas shows that the painter's eye (the horizon) was 4 ft. above the ground level.







