Domes, Turrets and Steeples - Draw in Perspective |
||||||||||||||||
|
Page 13 / 25
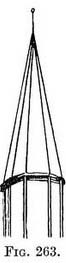
 CHAPTER XII 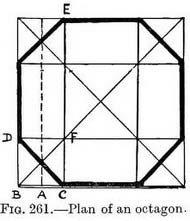 CONCERNING DOMES, TURRETS, AND STEEPLES OTHER THAN THOSE DESCRIBED IN CHAPTER XIAN octagonal steeple on a square tower. — An octagon has eight sides of equal length (Fig. 261). If enclosed in a square, four of its sides would lie on the middle portion of the sides of the square, the other four sides would cut across the corners. If then we find the length of one of its sides, we can construct the others by means of the square. In Fig. 261 the point A is at the end of a (dotted) line which cuts the diagonals at the same points as a circle would if inscribed in the square (explained fully in Chap. VII). The point C is the same distance from A 2 as A is from B. The point D is the same distance from B as C is, and it is found by drawing the line C–E, and at its intersection with the diagonal FIG. 261.—Plan of an octagon. the line F–D. The other corners of the octagon are found in the same way. To draw a foreshortened octagon. — Practice.—Draw a foreshortened square, find the point A, then the point C (by making C–A equal to B–A), then use the line C–E as in similar circumstances described in Chap. VII. The octagonal steeple. — Draw the foreshortened under side of a flat roof on top of the tower ; on it construct the foreshortened octagon ; from each corner raise sides that meet a central vertical pole at the appropriate height (Fig. 262). An octagonal tower and steeple. — Practice. — Draw its octagonal roof and steeple as in the last example. From each corner seen drop uprights to form its sides. Continue the roof sides to horizon to find the V.P.'s for each side ; use these for all sets of parallel lines such as where the tower touches the ground, window-sills, and drip-stones, courses of masonry, and strings (Fig. 263).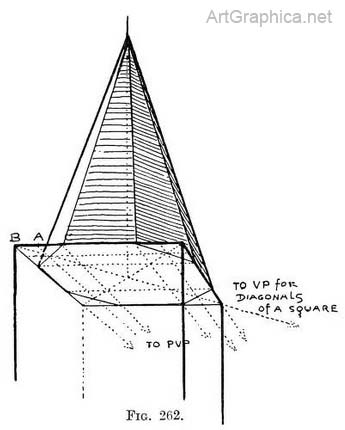 
Fig. 264 represents an octagonal dome and turret surmounting a square tower.
Practice. Draw a foreshortened square to represent the underside of a flat roof to the tower. Inside this (see " concentric squares ") form a smaller one ; raise the latter and form an octagon on it. Join the corner of the octagon with the tower corners, and allow for eaves. Any exercise with the octagon can be simplified by remembering that if four of its sides lie on a square, the remaining four sides lie at an angle of 45 degrees with the sides of the square. We should apply this in a front view of a tower by taking the near sides of the octagon that cut across the corners to the V.P. for diagonals ; one to the left, one to the right. If by chance the far sides should be visible, remember they use the same V P 's as the near sides (i.e. the far side on the right is parallel to the near side on the left, and so it uses the " diagonal " V.P. on the left, etc. (Fig. 266).
Practice (Fig. 267). — Draw ceiling of tower and on it an octagon. Raise central upright. Form pyramid roof A, B, C. Cut off at D, E. Raise spire from corners of octagon. Join " E " the centre of one face of the spire with 2 and 3 its base. It is already joined to the corner of the tower F.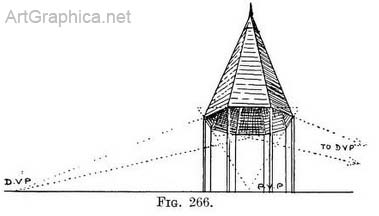 
An octagonal spire on a round tower. — We see from the plan (Fig. 270) that if a circle is inscribed in an octagon, it touches it at the middle of each of its sides. We know how to find these points (1 and 2) from our familiarity with the circle (Chap. VII). We also recognise that the corner B is found by the intersection of the line from C with the diagonal (Chap. IV).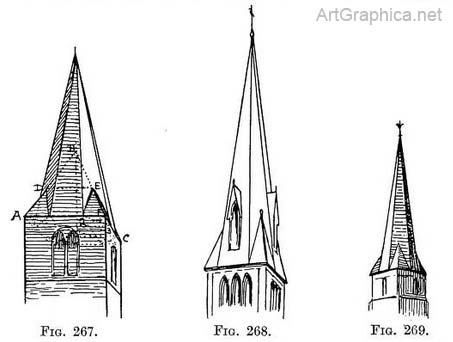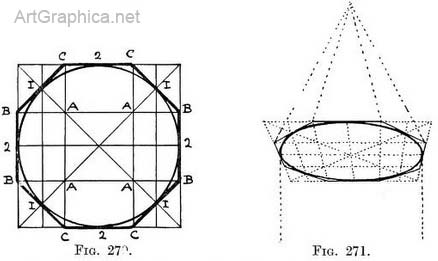  
Practice (Fig. 271). — Tick off from the plan, Fig. 270, the points X in order to locate B by means of intersection of diagonal at A. Refer to Figures 261, 262 and explanation if you find this one insufficient. A dome (Fig. 273).—Practice.—Make a plan of half a circle (A) ; on it mark off divisions required. Draw outline of dome, and across (the middle of) its base the line 1, on this transfer divisions from line 2 of plan. From P.V.P. carry lines to extremities of line 1 and continue them to form sides of a foreshortened square, on which the dome rests. - From P.V.P. carry lines through each division of line 1 ; construct circle. Mark where lines radiating from P.V.P. cut circle, and from each division on the circle draw, freehand, the lines from base to apex of dome ; carry these (divisions on the circle) vertically downwards also if columns are present.
The depths of the:perspective square is found by a line (2) from its centre (the intersection of the central vertical, with the horizontal middle line) to D.V.P. A door as it is opened travels on the circumference of a circle.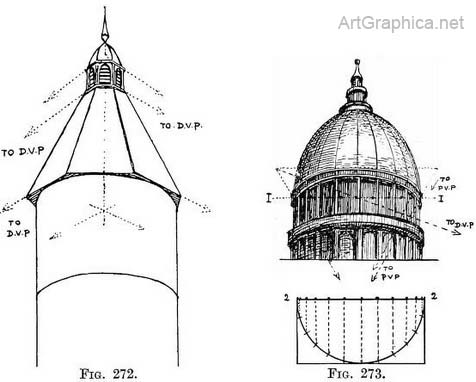 
Any projection on the bottom of the door would scrape a portion of a circle on the floor ; another from its top might mark a circle on the ceiling. Remembering this we could, but we do not, draw one circle above another by imitating the motion of the door.
If the outer top corner had been rounded the door would have resembled half a dome (Fig. 275). If such a door were opened at equal intervals, each representation of it would give the exact curve of the lines that run from the apex of a dome to its base.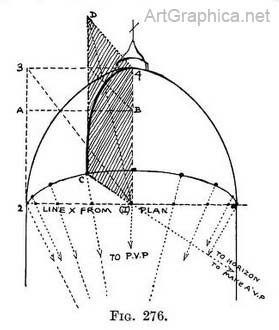 
Practice (Fig. 276). — Draw the outline of the dome and the foreshortened circle it stands on. Divide the near side of the circle into spaces that on the plan would be equal. On the centre of the circle swing a rectangular flap 1, 2, 3, 4 ; draw a diagonal across it (3-1), and where the diagonal touches the dome draw a horizontal line A, B. Now construct a foreshortened flap by first joining one of the divisions on the circular base with the centre of the circle C-1. Continue this line to the horizon to find V.P. join V.P. with the top of the pivot (4), and continue it to D, join D to C.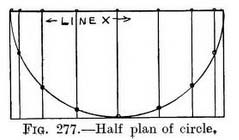 
Next Page
Sky in Perspective Prev Page Architectural Drawing
|
||||||||||||||||
Composite octagon spire (Fig. 265). — An octagon spire not rising directly from the tower which is of larger dimension than the base of the octagon—but joined to it by another roof.
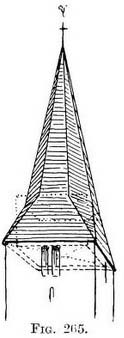Details of the same. — An octagonal spire is often set on a square tower with merely a tablet in place of a parapet. Examples of this are given in Figs. 267, 268, 269. Then the triangle left between the face of the spire where it cuts across the tower corner is filled by two sloping sides that taper and meet on the centre of the spire-face. These are the visible parts of the " squinches " or small arches which cross the tower corners and support the octagonal spire. There may be gabled lights on the faces of the spire, as are shown in Fig. 268. They present no new problems, being similar to a gabled roof-window.
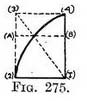
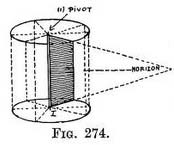Practice (Fig. 274). — First draw a foreshortened circle ; find its centre, and on it raise an upright for the door to swing on (1). From the centre of the circle rule a line to the circumference (to make the bottom
edge of the door), and continue it to the horizon to find the V.P. ; join the V.P. with the (2) upright pivot to make the top edge of door. Join the bottom edge where it touches the circumference to the top edge. Repeat this operation to represent the door at various angles. Use all the outer top corners as guiding points for the circle, and it will be correct in perspective in relation to the other circle below.
 |
Online Art Books
Perspective for Artists Art Lessons Free Art Books Art Shop Art Links  
 |
